Magnetohydrodynamics (MHD)

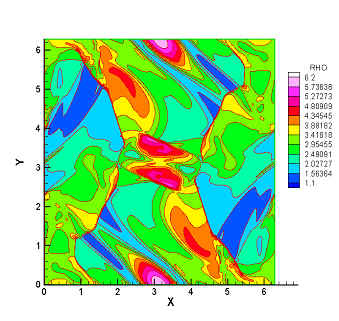
Ideal Magnetohydrodynamic (MHD) equations are obtained by coupling the Euler equations for flow motions in conjunction with the Maxwell equations for the electromagnetic fields. The ideal MHD equations consist of the continuity equation, the momentum equations, the energy equation and the magnetic induction equations. Moreover, a constraint of divergence-free condition of magnetic field (ΡΧB=0) is required according to Maxwell equations. The electro- magnetic effect on the charged fluid is manifested via Lorentz force, which modifies the momentum and energy equations. Due to evolving Lorentz force, wave structures in MHD flows are much more complex than that in pure gas. The MHD simulation is a challenge to CFD methods. In the numerical study of MHD equations with the CESE method, no reconstruction procedure or Riemann solver, and  special treatment for keeping ΡΧB=0 is needed.

Results